貪婪演算法可以解決的一個問題就是找到一張圖中的最小生成樹(minimum spanning tree)。

樹、生成樹與最小生成樹

我們之前提到資料結構中的樹是有根樹(rooted tree)，也就是樹中有一個根節點。但其實樹不一定都有根節點，只要任意兩節點都有(也只有)一條邊相連的圖就稱作樹。

圖片來源：維基百科

而一個圖中的生成樹(spanning tree)，就是指連接該圖所有節點的樹，一個圖可能有不只一個生成樹。而最小生成樹就是指在有權圖中，權重總和最小的生成樹。例如下圖中綠色的部分，就是這個圖的最小生成樹。

圖片來源：維基百科

那麼最小生成樹可以解決什麼問題呢？其中一種最直接的應用是線路設計，例如沿著街道(邊)為住家(節點)架設電纜的情境，最小生成樹可以作為成本最低的路徑。另外，最小生成樹也可以用來作為困難問題的近似解，或間接應用在人臉或字跡辨識等技術中。

貪婪解法

有許多演算法可以找到一個圖中的最小生成樹，下面寫到的幾種都是屬於貪婪演算法。這幾種方法雖然關注點或出發點不同，但同樣都是用貪婪策略，每一階段都選擇局部最佳解，以達到最終的整體最佳解。也表現出之前提到的，一個問題可能以多種貪婪演算法解決。

Prim's algorithm

普林演算法的策略與先前提到尋找最短路徑的Dijkstra演算法非常相似(事實上這個演算法也被Dijkstra再次發現與發表，所以也稱為Prim–Dijkstra algorithm)，它的作法是：

1. 先將任意節點加入到樹之中。

2. 選擇與樹距離最近的節點，加入到樹中，反覆此步驟直到所有節點均在樹中，即為最小生成樹。

以上方的圖為例，如果一開始選擇G節點，接下來將最近的節點E加入樹中，接下來將與G或E最近的節點C加入...以此類推，也就是每一階段樹都會納入距離最近的節點、增加一條邊，直到連接所有的節點。

Kruskal's algorithm

Kruskal演算法的方式是從所有邊中，反覆選擇最短的邊，它的步驟是：

1. 將所有的邊依照權重由小到大排序。

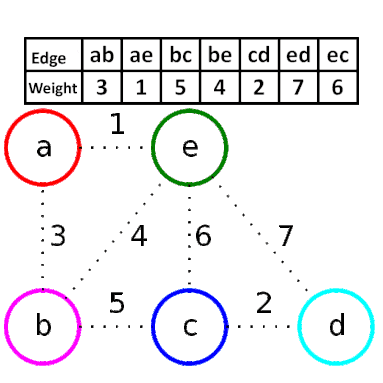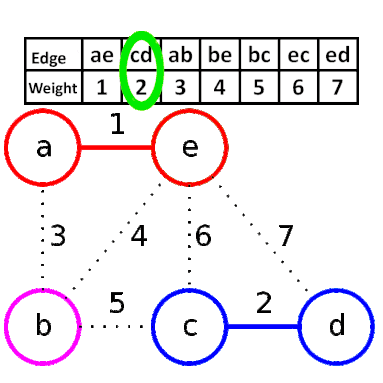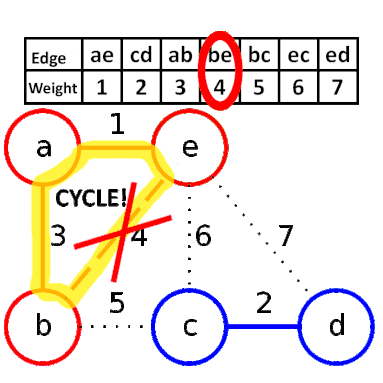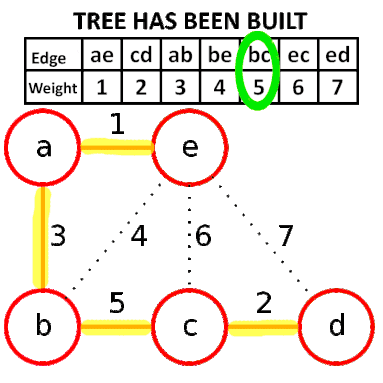
2. 從最小開始，選擇不會形成環的邊，直到連接所有節點。

如下圖，先將邊排序，依序選擇，其中邊be即是因為會形成環所以不選。

圖片來源：維基百科

Borůvka's algorithm

Borůvka演算法則是利用節點的最短邊得出多棵樹，再將樹以最短邊相連：

1. 找尋每個節點的最短邊，可以重複選擇(例如下圖AC同時是A節點和C節點的最短邊)，如此一來會形成幾個不相連的樹，如下圖中經過第一步驟後得到AC、BD、EF等不同的樹，以不同顏色標示。
2. 以同樣的方式，反覆找尋每個樹的最短邊，每次操作樹的數量都會減少，直到最終只剩下一個樹即為最小生成樹。

圖片來源：維基百科